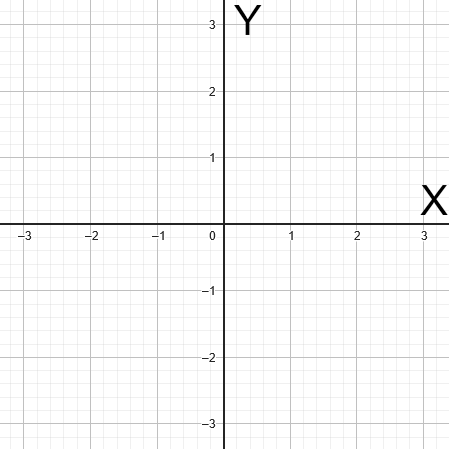Kartesisches Koordinatensystem

Das kartesische Koordinatensystem, benannt nach dem französischen Mathematiker René Descartes, ist ein mathematisches Konzept, das zur Darstellung von Punkten in einem zweidimensionalen oder dreidimensionalen Raum verwendet wird. Es besteht aus zwei Achsen, die senkrecht zueinander stehen.

Im zweidimensionalen kartesischen Koordinatensystem gibt es zwei Achsen: die X-Achse und die Y-Achse. Die X-Achse verläuft horizontal und die Y-Achse verläuft vertikal. Der Punkt, an dem sich die beiden Achsen schneiden, wird als Ursprung bezeichnet und wird mit dem Koordinatenpaar (0, 0) dargestellt.

Um einen Punkt im Koordinatensystem zu bestimmen, werden die x- und y-Koordinaten verwendet. Die x-Koordinate gibt die horizontale Position des Punktes relativ zum Ursprung an, während die y-Koordinate die vertikale Position angibt.

Positive x-Koordinaten werden nach rechts gemessen und negative x-Koordinaten nach links. Positive y-Koordinaten werden nach oben gemessen und negative y-Koordinaten nach unten.

Punkte im Koordinatensystem werden üblicherweise in der Form (x, y) notiert, wobei x die x-Koordinate und y die y-Koordinate des Punktes ist. Beispielsweise liegt der Punkt (2, 3) zwei Einheiten nach rechts und drei Einheiten nach oben vom Ursprung entfernt.

Das dreidimensionale kartesische Koordinatensystem erweitert das zweidimensionale System um eine zusätzliche Achse, die z-Achse. Die z-Achse verläuft senkrecht zur xy-Ebene und ermöglicht die Darstellung von Punkten im dreidimensionalen Raum. Die z-Koordinate gibt die Position entlang der z-Achse an.

Das kartesische Koordinatensystem ist eine grundlegende Methode zur Darstellung und Analyse von geometrischen Formen, Linien, Flächen und Vektoren in der Mathematik und Physik. Es bildet die Grundlage für viele mathematische Konzepte wie Geometrie, lineare Algebra und Analytische Geometrie.